AI dla każdego. Część 4.

Poprzednią część zakończyłem omówieniem podstaw działania perceptronu – najprostszej sieci neuronowej. Teraz nadeszła pora na wyjaśnienie najbardziej „magicznej” właściwości sztucznej inteligencji – tego, że sieci neuronowe potrafią się uczyć.

Nauka nadzorowana (z trenerem) i ważenie danych

W poprzedniej części opisałem działanie sztucznego neuronu i mechanizmu wag. Dla przypomnienia, waga to fundamentalny element neuroplastyczności w sztucznych sieciach neuronowych. Waga to liczba, która określa ważność (wagę) wejścia, do którego jest przypisana. Im wyższa waga, tym większe znaczenie ma sygnał na wejściu i nawet jego niewielkie zmiany będą wywierać duży wpływ na sygnał na wyjściu neuronu. Im waga niższa, tym mniejsze znaczenie będą miały nawet duże wahania sygnału przypisanego do wejścia z taką wagą. Ale skąd sztuczny neuron „wie”, jakie wagi są przypisane poszczególnym wejściom? Jedną z możliwości jest wcześniejsze, wstępne zaprogramowanie wag przez człowieka. Innym sposobem, spotykanym najczęściej w nienadzorowanym uczeniu się, jest losowanie wartości wag z ustalonego wcześniej zakresu. Manipulowanie wartościami wag na podstawie sygnału zwrotnego jest istotą procesu nauki w sztucznych sieciach neuronowych. Takim sygnałem zwrotnym jest błąd.

Mylić się jest rzeczą nie tylko ludzką

Człowiek nie jest doskonały i, jak mówi mądre powiedzenie, uczy się przez całe życie, choć niestety często na własnych błędach. Tak jednak działa jego mechanizm poznawczy. Dzięki temu, że uczymy się unikać takich błędów, które już kiedyś popełniliśmy, lub przynajmniej je minimalizować, rozwijamy się i stajemy się doskonalsi. To jedna z podstawowych sił napędowych ewolucji – rozwiązania lub osobniki słabe, które nie sprawdzają się lub nie radzą sobie w rzeczywistych warunkach są w sposób naturalny eliminowane na rzecz rozwiązań i osobników lepszych, silniejszych. Dokładnie ta zasada legła u podstaw algorytmu genetycznegoI, który został zdefiniowany przez Johna Henry'ego Hollanda w 1960 r^II. Algorytm genetyczny należy do grupy algorytmów ewolucyjnych, czyli rozwiązań wzorowanych na ewolucji biologicznej, i jest stosowany tam, gdzie wymagana jest optymalizacja lub modelowanie obiektów bądź procesów. Sieć neuronowa jest doskonałym przykładem obiektu, który można modelować za pomocą algorytmów genetycznych. W jaki sposób działa taki algorytm? Na początku tworzona jest pewna liczba obiektów stanowiących populację startową. Obiekty z tej populacji mają ten sam zestaw parametrów, ale wartości tych parametrów dla populacji startowej są losowane. Następnie uruchamiany jest proces nauki, w którym obiekty populacji startowej wykonują założone zadanie, a ich parametry ulegają modyfikacjom na podstawie uzyskanych wyników. Kluczem do tych modyfikacji jest nauka na własnych błędach. Błędem w tym przypadku jest nieosiągnięcie oczekiwanego wyniku – im większe odchylenie, tym większy jest błąd. Posłużę się tu przykładem prostej gry w wyścigi, rozgrywanej na dwuwymiarowej planszy – wirtualnym torze wyścigowym. Populacja będzie się składać ze stałej liczby wirtualnych pojazdów, powiedzmy dziesięciu, a ich zadaniem będzie przejechanie przypisanych im wirtualnych torów w taki sposób, aby nie najechać na krawędź toru. Każdy pojazd jedzie po swoim własnym torze, takim samym jak tor każdego innego. Gra składa się z wielu wyścigów, które są powtarzane tak długo, aż któryś z pojazdów nauczy się pokonywać tor bezkolizyjnie i możliwie najszybciej. Oczywiście taki pojazd będzie zwycięzcą gry. Ewolucja obiektów populacji startowej będzie polegała na analizowaniu błędów popełnionych przez pojazdy – każde zetknięcie się z krawędzią toru będzie sygnałem zwrotnym dla neuronów sztucznej sieci neuronowej, informującym o konieczności modyfikacji parametrów jazdy w kolejnym wyścigu. Każdy z pojazdów ma ten sam zestaw właściwości i procedur. Właściwościami pojazdu są aktualna pozycja X i Y, bieżąca prędkość własna oraz aktualny kierunek jazdy. Procedurami pojazdu są natomiast skręt w lewo, skręt w prawo i zmiana prędkości. Pojazdy nie znają przebiegu trasy wyścigu i muszą go poznać. Każdy kolejny wyścig pozwala zebrać informacje o popełnionych błędach i tak zmodyfikować procedury sterowania pojazdem (wagi neuronów w poszczególnych warstwach sieci), aby ten sam błąd nie wystąpił podczas kolejnego wyścigu. Po każdym wyścigu mamy do czynienia z nową generacją pojazdów – bogatszą o doświadczenia poprzedniej generacji, dokładnie tak jak w procesie ewolucji naturalnej.

Wzmocnienie

Warto omówić przypadek działania systemu sztucznej inteligencji, w którym zachodzi konieczność zmiany progu zadziałania neuronu lub grupy neuronów, a jednocześnie zmiana wartości poszczególnych wag na wejściach jest niepożądana. Przykładowo, w systemie rozpoznawania kolorów nagłe zwiększenie jasności obrazu na wejściu spowoduje przesunięcie się palety barw w stronę kolorów jaśniejszych, co dla systemu wytrenowanego przy zupełnie innej jasności może stanowić problem. Rozwiązaniem jest sztuczny neuron z dodatkowym wejściem wzmocnienia o nazwie bias, przedstawiony na rys. 1.

Rys. 1. Sztuczny neuron z dodatkowym wejściem wzmocnienia bias. Graf.: P. Rogalewski

Im silniejszy sygnał jest podawany na wejście bias, tym większe będzie wzmocnienie sygnałów na wejściach synaptycznych (wszystkie te wejścia staną się bardziej czułe na sygnały wejściowe – w jednakowym stopniu) i odwrotnie – im słabszy sygnał na wejściu bias, tym mniejsza czułość wejść synaptycznych neuronu. Innymi słowy, próg zadziałania funkcji aktywacji neuronu będzie przesuwał się w górę albo w dół w zależności od wartości sygnału na wejściu bias. W opisanym wyżej przykładzie z paletą barw nagłe zwiększenie jasności obrazu można skompensować, podając ujemny sygnał na wejście wzmocnienia w celu obniżenia czułości neuronów na poszczególne analizowane barwy.

Wsteczna propagacja błędu i reguła delta

Pozostaje odpowiedzieć na pytanie: skąd neuron wie, że popełnił błąd i jak duży był to błąd? Wyjaśnienie znajduje się na rys. 2.

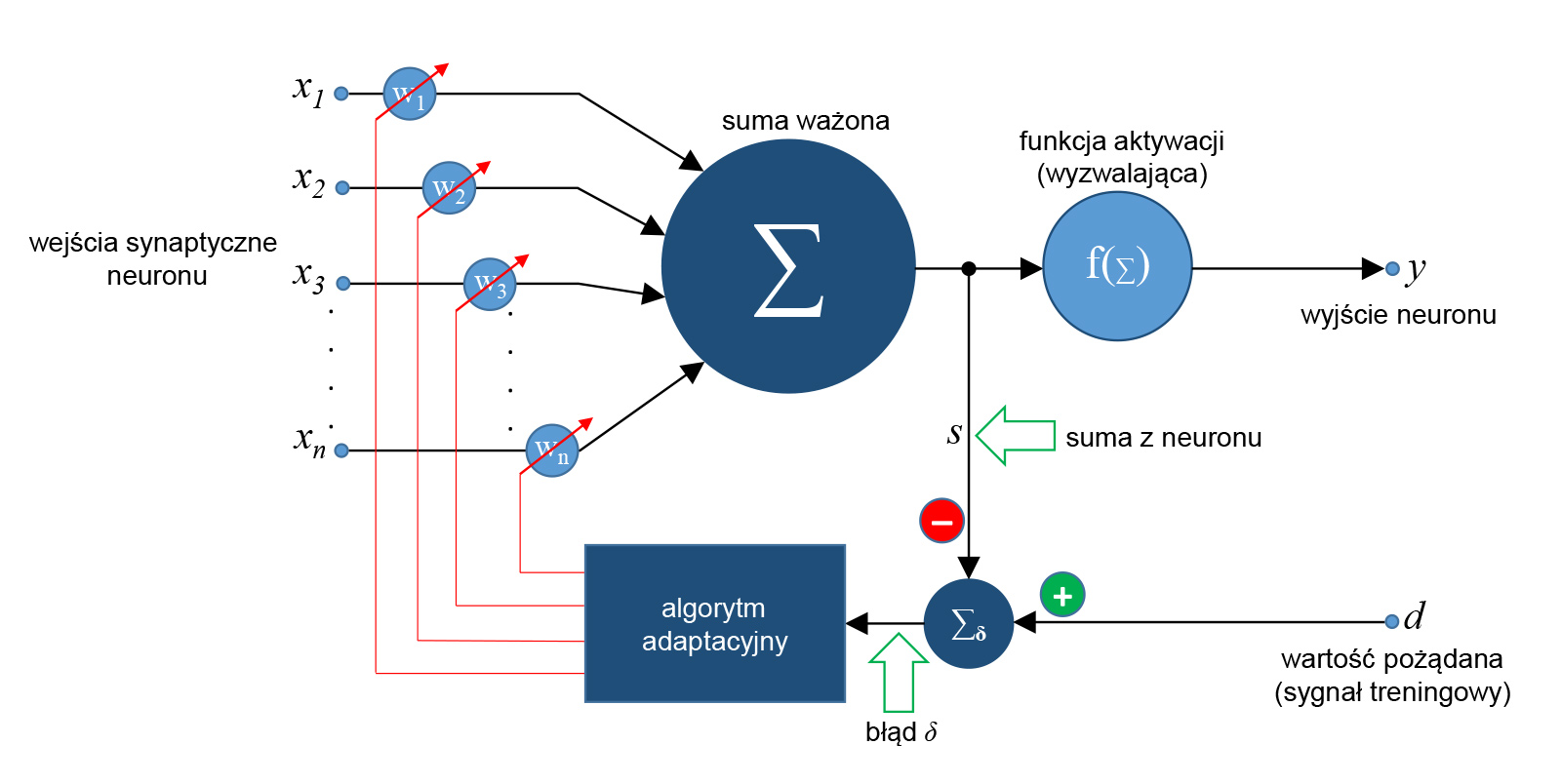
Rys. 2. Neuron liniowy typu ADALINE z mechanizmem adaptacji wag. W celu uzyskania odpowiedniej czytelności rysunku pominięto wejście wzmocnienia bias. Graf.: P. Rogalewski

Oprócz opisanych w poprzedniej części cyklu AI dla każdego standardowych wejść synaptycznych x1… xn i wyjścia y neuron posiada dodatkowe wejście d, do którego doprowadzony jest sygnał wzorcowy. Tego typu neuron jest adaptacyjnym neuronem liniowym nazywanym ADALINE (od ang. Adaptive Linear Neuron)^III. Neuron jest nazywany liniowym, ponieważ jego funkcja aktywacji jest funkcją liniową. Sieć neuronowa składająca się z wielu neuronów ADALINE to MADALINE (od ang. Many Adaptive Linear Neurons). Obecnie jest ona jednym z najpopularniejszych i najpowszechniej stosowanych typów sieci. Sygnałem wzorcowym d jest wartość, jaka jest oczekiwana na wyjściu neuronu w odpowiedzi na określony zestaw sygnałów wejściowych. Innymi słowy jest to pozytywny (jako wzorzec, nie matematycznie), wzorcowy sygnał „treningowy” (oznaczony na rysunku zielonym symbolem „+”), który „mówi” neuronowi, że to jest wartość, do której powinien dążyć. Neuron oblicza różnicę wartości sygnału treningowego d i wyliczonej przez siebie sumy ważonej s (na rysunku czerwony znak „-” określający sygnał typu negatywnego), określając tym samym wielkość błędu ? (delta). Proces ten to tzw. reguła delta stanowiąca fundament procesu uczenia neuronów. Reguła ta jest opisana wzorem:

δ = d – s

Im większy błąd, tym większa wartość δ. Następnie wartość sygnału błędu δ jest przekazywana jako argument wejściowy dla algorytmu, który manipuluje wagami, dostrajając je tak, by wartość błędu na wyjściu neuronu zminimalizować. Im większy błąd, tym mocniejsze dostrojenie jest potrzebne. Cały proces uczenia neuronów sprowadza się właściwie do minimalizacji błędu średniokwadratowego w poszczególnych warstwach sieci i w pojedynczych neuronach. Jak łatwo zauważyć, błędy są w tym przypadku informacją biegnącą w kierunku przeciwnym do kierunku działania neuronu. Sygnały wejściowe x wejść synaptycznych ulegają propagacji, czyli biegną od lewej do prawej strony neuronu i „w głąb” sieci neuronowej. Informacje o błędach „podróżują” natomiast w przeciwną stronę – „w górę”, między warstwami sieci (neurony przekazują sobie informację o błędach), jak i w samym neuronie (od prawej do lewej). Ta odwrócona wędrówka sygnałów to wsteczna propagacja błędu. Uczenie sieci uznaje się za zakończone, gdy wszystkie neurony w poszczególnych warstwach sieci dostroją swoje wagi tak, by na wyjściu generować sygnały jak najbardziej zbliżone do wzorców treningowych.

Co za dużo, to niezdrowo

W przypadku sztucznej inteligencji, podobnie jak w naturze, przesada nie jest wskazana. Przetrenowany sportowiec może nabawić się kontuzji i stracić motywację do dalszej ciężkiej pracy, zamiast osiągnąć lepszy wynik. Analogicznie, przetrenowana (ang. overtrained) sieć neuronowa będzie działać mniej efektywnie, a nawet niezgodnie z przewidywaniami^IV. Często takie zjawisko nazywa się także nadmiernym dopasowaniem (ang. overfitting). Z czego to wynika? Jeśli opisana wyżej procedura manipulacji wagami zostanie wykonana zbyt precyzyjnie i wagi zostaną dostrojone zbyt „wąsko”, bez odpowiedniej tolerancji, sieć będzie reagować zbyt „ostro” na dane wejściowe i w efekcie przez filtry klasyfikacji będzie przechodził tylko niewielki zbiór obiektów. Aby lepiej to wyjaśnić, wrócę do przykładu kota, który podałem w drugiej części (nr 2/2019 „Zabezpieczeń”). Gdyby sieć neuronowa została wytrenowana zbyt dużą liczbą zdjęć śpiących kotów zwiniętych w kłębek, nie byłaby w stanie prawidłowo rozpoznać kotów stojących na łapkach. Dobór materiału treningowego oraz określenie momentu, w którym należy zakończyć uczenie sieci, jest jednym z najtrudniejszych wyzwań dla twórców systemów sztucznej inteligencji.

W kolejnym artykule opiszę przykładowe rozwiązania implementujące sieci neuronowe i systemy deep learning.

Piotr Rogalewski

Przypisy:

1. Pojęcie algorytmu zostało wyjaśnione w drugiej części cyklu AI dla każdego („Zabezpieczenia” nr 2/2019).
2. D. E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning, Addison-Wesley Professional, Boston 1989.
3. B. Widrow, M. A. Lehr, 30 Years of Adaptive Neural Networks: Perceptron, Madaline, and Backpropagation, (w:) Proceedings of the IEEE, vol. 78, nr 9, wrzesień 1990, s. 1415–1442.
4. I. V. Tetko, D. J. Livingstone, A. I. Luik, Neural Network Studies. 1. Comparison of Overfitting and Overtraining, (w:) „Journal of Chemical Information and Computer Sciences”, nr 35, wrzesień 1995, s. 826–833.